Ridge regression
Ridge regression is a linear regression technique that addresses multicollinearity and overfitting by adding a penalty term to the ordinary least squares method.
The objective function of ridge regression is given by:
\[ \min_{\mathbf{w} \in \mathbb{R}^d} \sum^n_{i=1}(\mathbf{w}^T\mathbf{x}_i-y_i)^2 + \lambda||\mathbf{w}||_2^2 \]
Here, \(\lambda||\mathbf{w}||_2^2\) serves as the regularization term, and \(||\mathbf{w}||_2^2\) represents the squared L2 norm of \(\mathbf{w}\). Let us denote this equation as \(f(\mathbf{w})\).
Alternatively, we can express ridge regression as:
\[ \min_{\mathbf{w} \in \mathbb{R}^d} \sum^n_{i=1}(\mathbf{w}^T\mathbf{x}_i-y_i)^2 \hspace{1em}\text{s.t.}\hspace{1em}||\mathbf{w}||_2^2\leq\theta \]
Here, the value of \(\theta\) depends on \(\lambda\). We can conclude that for any choice of \(\lambda>0\), there exists a corresponding \(\theta\) such that optimal solutions to our objective function exist.
The loss function for linear regression with the maximum likelihood estimator \(\mathbf{w}_{\text{ML}}\) is defined as:
\[ f(\mathbf{w}_{\text{ML}}) = \sum^n_{i=1}(\mathbf{w}_{\text{ML}}^T\mathbf{x}_i-y_i)^2 \]
Consider the set of all \(\mathbf{w}\) such that \(f(\mathbf{w}_{\text{ML}}) = f(\mathbf{w}) + c\), where \(c>0\). This set can be represented as:
\[ S_c = \left \{\mathbf{w}: f(\mathbf{w}_{\text{ML}}) = f(\mathbf{w}) + c \right \} \]
In other words, every \(\mathbf{w} \in S_c\) satisfies the equation:
\[ ||\mathbf{X}^T\mathbf{w}-\mathbf{y}||^2 = ||\mathbf{X}^T\mathbf{w}_{\text{ML}}-\mathbf{y}||^2 + c \]
Simplifying the equation yields:
\[ (\mathbf{w}-\mathbf{w}_{\text{ML}})^T(\mathbf{X}\mathbf{X}^T)(\mathbf{w}-\mathbf{w}_{\text{ML}}) = c' \]
The value of \(c'\) depends on \(c\), \(\mathbf{X}\mathbf{X}^T\), and \(\mathbf{w}_{\text{ML}}\), but it does not depend on \(\mathbf{w}\).
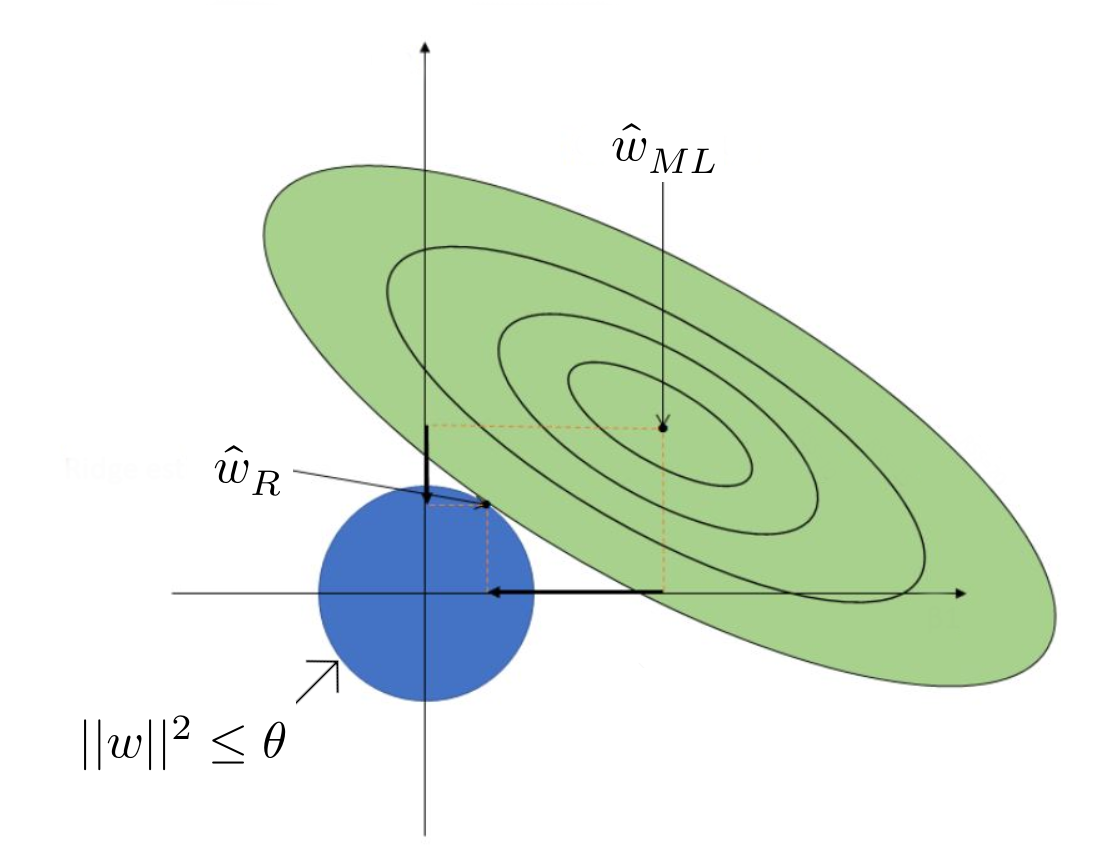
In summary, ridge regression regularizes the feature values, pushing them towards zero, but not necessarily to zero.