Lasso Regression

Lasso (Least Absolute Shrinkage and Selection Operator) regression is a linear regression technique that employs a regularization approach to shrink the coefficients of less important features to zero. This method effectively performs feature selection and mitigates overfitting.

The objective function of lasso regression is given by:

\[ \min_{\mathbf{w} \in \mathbb{R}^d} \sum^n_{i=1}(\mathbf{w}^T\mathbf{x}_i-y_i)^2 + \lambda||\mathbf{w}||_1^2 \]

Lasso regression is similar to ridge regression, with the key difference being the use of \(||\mathbf{w}||_1^2\) instead of \(||\mathbf{w}||_2^2\), representing the squared L1 norm of \(\mathbf{w}\).

Pictoral Representation of what Lasso Regression does.

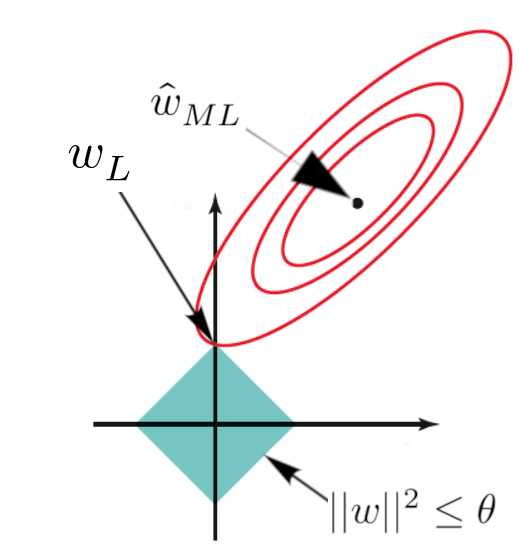
Lasso regression does not have a closed-form solution and is often solved using sub-gradients. Further information on sub-gradients can be found here.

In conclusion, lasso regression shrinks the coefficients of less important features to exactly zero, enabling feature selection.