Decision tree
Introduction
Decision trees are widely used in machine learning for classification and regression tasks. They operate by recursively partitioning the data based on the most informative features until a stopping criterion is met. Decision trees can be visualized as tree-like structures.
Consider a dataset \(\{\mathbf{x}_1, \ldots, \mathbf{x}_n\}\), where \(\mathbf{x}_i \in \mathbb{R}^d\), and let \(\{y_1, \ldots, y_n\}\) be the corresponding labels, where \(y_i \in \{0, 1\}\). The output of the decision tree algorithm is a constructed decision tree.
Prediction: Given a test sample \(\mathbf{x}_{\text{test}}\), we traverse the decision tree to reach a leaf node, and the label assigned to the leaf node is considered as \(y_{\text{test}}\).
The following diagram depicts a decision tree:
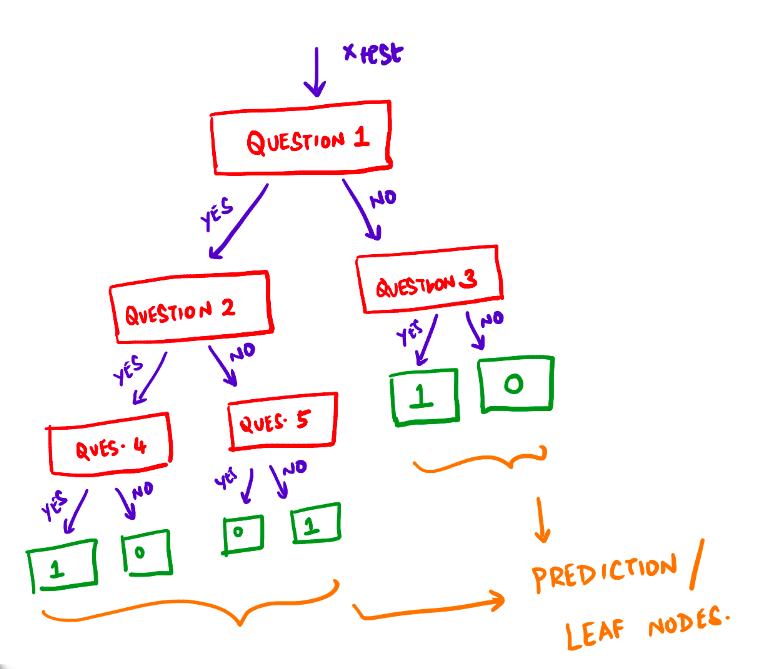
Here, a question refers to a (feature, value) pair. For example, \(height \le 180\text{cm}\)?
Goodness of a Question
To evaluate the quality of a question, we need a measure of “impurity” for a set of labels \(\{y_1, \ldots, y_n\}\). Various measures can be employed, but we will use the Entropy function.
The Entropy function is defined as:
\[ \text{Entropy}(\{y_1, \ldots, y_n\}) = \text{Entropy}(p) = -\left( p\log(p)+(1-p)\log(1-p) \right ) \]
Here, \(\log(0)\) is conventionally treated as \(0\).
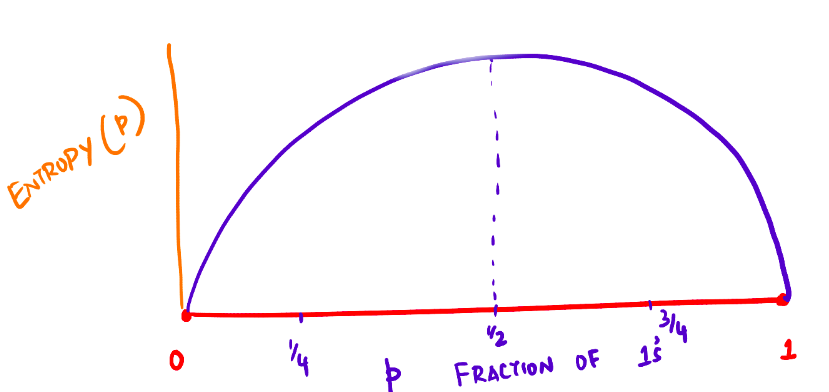
Pictorial representation of the Entropy function:
Information Gain is then utilized to measure the quality of a split in the decision tree algorithm.
Information gain is a commonly used criterion in decision tree algorithms that quantifies the reduction in entropy or impurity of a dataset after splitting based on a given feature. High information gain signifies features that effectively differentiate between the different classes of data and lead to accurate predictions.
Information gain is calculated as:
\[ \text{Information Gain}(\text{feature}, \text{value}) = \text{Entropy}(D) - \left[\gamma \cdot \text{Entropy}(D_{\text{yes}}) + (1-\gamma) \cdot \text{Entropy}(D_{\text{no}}) \right] \]
where \(\gamma\) is defined as:
\[ \gamma = \frac{|D_{\text{yes}}|}{|D|} \]
Decision Tree Algorithm
The decision tree algorithm follows these steps:
- Discretize each feature within the range [min, max].
- Select the question that provides the highest information gain.
- Repeat the procedure for subsets \(D_{\text{yes}}\) and \(D_{\text{no}}\).
- Stop growing the tree when a node becomes sufficiently “pure” according to a predefined criterion.
Different measures, such as the Gini Index, can also be employed to evaluate the quality of a question.
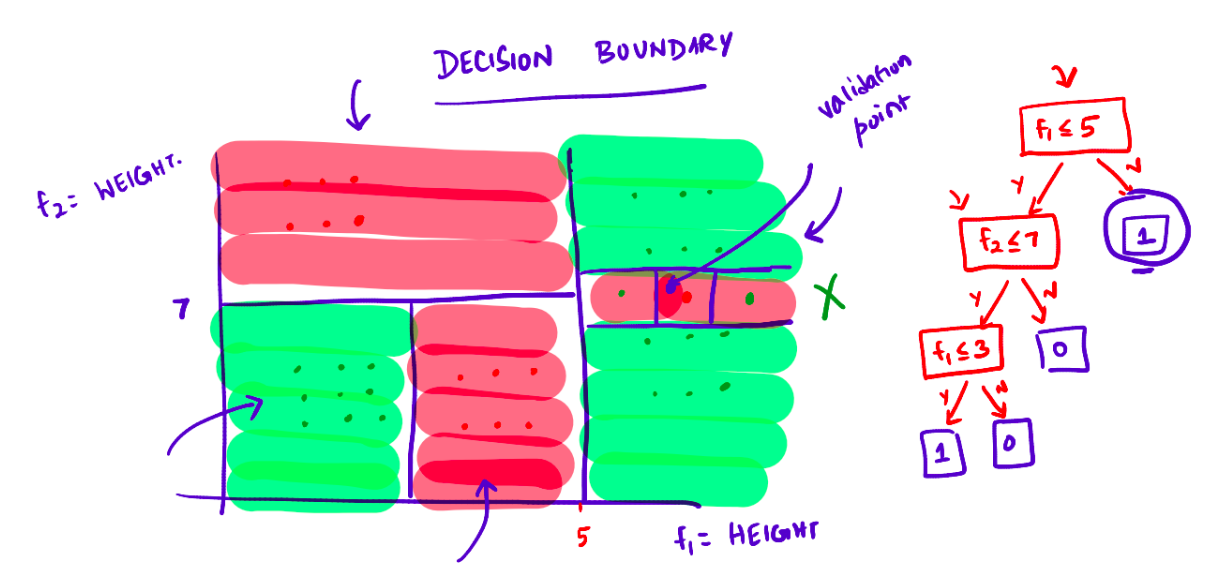
Pictorial depiction of the decision boundary and its decision tree: