Weight Initializations
Activation functions play a crucial role in introducing non-linearity to neural networks, enabling them to model complex relationships and learn intricate patterns from the data. Here are common activation functions used in neural networks:
| Activation | Formula | Graph | Description |
|---|---|---|---|
| Sigmoid | \(a = \frac{1}{1 + e^{-z}}\) | 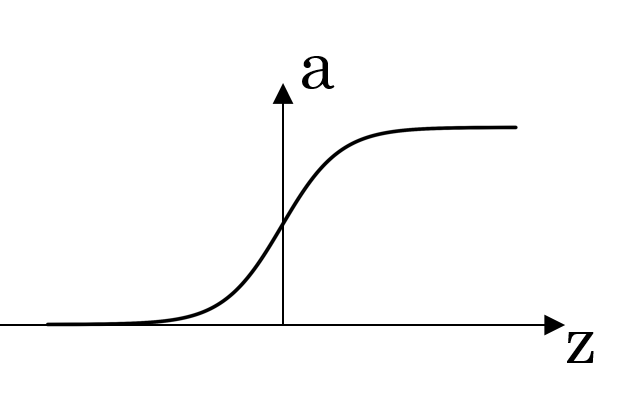 |
The sigmoid function produces outputs between 0 and 1, resembling an S-shaped curve. It’s suitable for binary classification tasks where the output needs to be in the range [0, 1]. |
| Tanh | \(a = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}}\) | 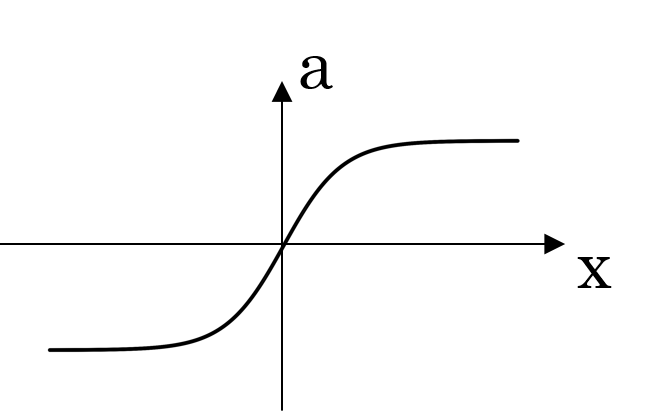 |
Tanh, or hyperbolic tangent, produces outputs between -1 and 1. It is similar to the sigmoid function but with outputs centered around zero, making it suitable for hidden layers. |
| ReLU (Rectified Linear Unit) | \(a = \max(0, z)\) | 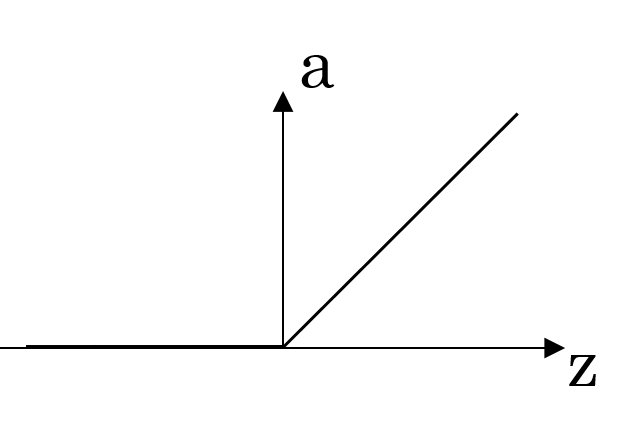 |
ReLU is a simple and widely used activation function that outputs zero for negative inputs and linearly increases for positive inputs, efficiently mitigating the vanishing gradient problem. |
| Leaky ReLU | \(a = \max(0.01z, z)\) | 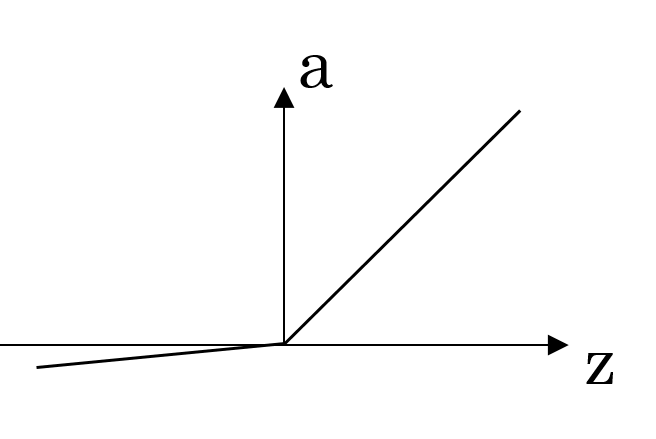 |
Leaky ReLU is an improved version of ReLU, allowing a small gradient for negative inputs to address the “dying ReLU” problem encountered with the standard ReLU function. |
Importance of Non-linear Activation Functions:
Neural networks with non-linear activation functions can approximate complex functions and relationships between inputs and outputs. Linear activation functions result in neural networks that are essentially just linear transformations, limiting their ability to capture intricate patterns present in real-world data.
A detailed explanation on Stack Overflow provides insights into the necessity of non-linear activation functions in enabling neural networks to learn complex mappings.
Derivatives of Activation Functions:
The derivatives of activation functions are essential for backpropagation during the training of neural networks. Here are the derivatives of common activation functions:
| Activation | Formula | Derivative |
|---|---|---|
| Sigmoid | \(a = \frac{1}{1 + e^{-z}}\) | \(a(1 - a)\) |
| Tanh | \(a = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}}\) | \(1 - a^2\) |
| ReLU | \(a = \max(0, z)\) | 0 if \(z < 0\); 1 if \(z \geq 0\) |
| Leaky ReLU | \(a = \max(0.01z, z)\) | 0.01 if \(z < 0\); 1 if \(z \geq 0\) |
Understanding these derivatives is crucial in computing gradients during backpropagation, facilitating the adjustment of weights and biases for effective training of neural networks.
These diverse activation functions empower neural networks to handle various types of data and learn complex relationships, contributing to their adaptability and efficiency in modeling intricate patterns within datasets.